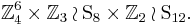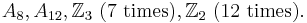Rubik's cube group
| Group theory |
|---|
| Group theory |
|
Cyclic group Zn
Symmetric group, Sn Dihedral group, Dn Alternating group An Mathieu groups M11, M12, M22, M23, M24 Conway groups Co1, Co2, Co3 Janko groups J1, J2, J3, J4 Fischer groups F22, F23, F24 Baby Monster group B Monster group M |
|
|
|
Solenoid (mathematics)
Circle group General linear group GL(n) Special linear group SL(n) Orthogonal group O(n) Special orthogonal group SO(n) Unitary group U(n) Special unitary group SU(n) Symplectic group Sp(n) Lorentz group Poincaré group Conformal group Diffeomorphism group Loop group Infinite-dimensional Lie groups O(∞) SU(∞) Sp(∞) |
The Rubik's Cube group is a mathematical group which corresponds to the set of all cube operations on Rubik's Cube, with function composition (chaining moves) as the group operation.
Any set of operations which returns the cube to the solved state, from the solved state, should be thought of as the identity transformation (the operation that does nothing). Any set of operations which solves the cube from a scrambled state should be thought of as an inverse transformation of the given scrambled state, since it returns the identity transformation.
Contents |
Formal description
Group axioms
The Rubik's cube shares the axioms with mathematical groups: identity, inverse, closure, associativity. It has an identity, simply not manipulating the cube. It has an inverse: by reversing a move sequence, the cube will return to its original position. It has closure: simpler sequences of moves combine to form a more complex move. Finally, it has associativity because doing different moves together, but in the same order, does not change the pattern.
Objects
Formally, the Rubik's Cube group can be best understood as a permutation group. A 3×3×3 Rubik's cube consists of 6 faces, each with 9 colored squares called facets for a total of 54 facets. As the 6 facets in the centre of the faces are not moved by any cube operation, there are a total of 48 facets which actually change position.
Rotations of the centre facets are unimportant on the standard cube, but are crucial when considering non-standard incarnations such as Rubik's calendar and Rubik's world.
Operations
The cube operations consist of rotating the 6 faces and thereby permuting the 48 movable facets. By definition, each element of the cube group is a permutation of the 48 movable facets. However, there is a one-to-one correspondence between elements of the cube group and legal positions of the Rubik's cube. Any element of the cube group is a permutation that when applied to the solved cube results in a (legal) cube position. Conversely, any legal cube position must be the result of some sequence of face rotations applied to the solved cube, and any such sequence composition is an element of the cube group. The cube group G can then be defined as the subgroup of the full symmetric group S48 generated by the 6 face rotations.
Total number
The order of the cube group G is then equal to the number of possible positions attainable by the cube. This is:
which factors to
Because of the large size of the cube group, it is sometimes useful to analyse the structure with the assistance of a computer algebra system.
Structure
In the following, we assume the notation described in How to solve the Rubik's Cube. Also we assume the orientation of the six centre facets to be fixed.
We consider two subgroups of G: First the group of cube orientations, Co, which leaves every block fixed, but can change its orientation. This group is a normal subgroup of G. It can be represented as the normal closure of some operations that flip a few edges or twist a few corners. For example, it is the normal closure of the following two operations:
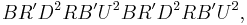 (twist two corners)
(twist two corners)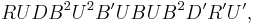 (flip two edges).
(flip two edges).
For the second group we take G permutations, Cp, which can move the blocks around, but leave the orientation fixed. For this subgroup there are more choices, depending on the precise way you fix the orientation. One choice is the following group, given by generators (the last generator is a 3 cycle on the edges):
Since Co is a normal subgroup, the intersection of Co and Cp is the identity, and their product is the whole cube group, it follows that the cube group G is the semi-direct product of these two groups. That is
(For technical reasons, the above analysis is not correct. However, the possible permutations of the cubes, even when ignoring the orientations of the said cubes, is at the same time no bigger than Cp and at least as big as Cp, and this means that the cube group is the semi-direct product given above.)
Next we can take a closer look at these two groups. Co is an abelian group, it is
Cube permutations, Cp, is little more complicated. It has the following two normal subgroups, the group of even permutations on the corners A8 and the group of even permutations on the edges A12. Complementary to these two groups we can take a permutation that swaps two corners and swaps two edges. We obtain that
Putting all the pieces together we get that the cube group is isomorphic to
This group can also be described as the subdirect product ![[(\mathbb Z_3^7 \rtimes \mathrm S_8) \times (\mathbb Z_2^{11} \rtimes \mathrm{S}_{12})]^\frac{1}{2}](/2012-wikipedia_en_all_nopic_01_2012/I/a61e29e2da7af0c37e11b6f35167bb2f.png) , in the notation of Griess.
, in the notation of Griess.
Generalizations
When the centre facet symmetries are taken into account, the symmetry group is a subgroup of
(This unimportance of centre facet rotations is an implicit example of a quotient group at work, shielding the reader from the full automorphism group of the object in question.)
The symmetry group of the Rubik's cube obtained by dismembering it and reassembling is slightly larger: namely it is the direct product
The first factor is accounted for solely by rotations of the centre pieces, the second solely by symmetries of the corners, and the third solely by symmetries of the edges. The latter two factors are examples of wreath products.
The simple groups that occur as quotients in the composition series of the standard cube group (i.e. ignoring centre piece rotations) are
References and external links
- Structure mathématique du Rubik's Cube.
- David Joyner (2002). Adventures in Group Theory : Rubik's Cube, Merlin's Machine, and Other Mathematical Toys. The Johns Hopkins University Press. ISBN 0-8018-6947-1. Notes from an earlier version of this book are available online at [1].
- Martin Schönert "Analyzing Rubik's Cube with GAP": the permutation group of Rubik's Cube is examined with GAP computer algebra system
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
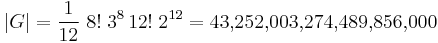
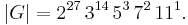
![C_p = [U^2, D^2, F, B, L^2, R^2, R^2 U^\prime F B^\prime R^2 F^\prime B U^\prime R^2].\,\!](/2012-wikipedia_en_all_nopic_01_2012/I/bf6978cf4bba6e598dddec888812e25d.png)
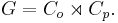
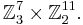
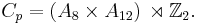
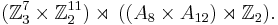
![[\mathbb Z_4^6 \times (\mathbb Z_3^7 \rtimes \mathrm S_8) \times (\mathbb Z_2^{11} \rtimes \mathrm S_{12})]^\frac{1}{2}.](/2012-wikipedia_en_all_nopic_01_2012/I/4685ce0b9b9a788a3bc9234424ba1d4b.png)